BZOJ4621:TC605

题目传送门

【BZOJ4621】Tc605_supreme567的博客-CSDN博客

Description

最初你有一个长度为 N 的数字序列 A。为了方便起见，序列 A 是一个排列。
你可以操作最多 K 次。每一次操作你可以先选定一个 A 的一个子串，然后将这个子串的数字全部变成原来这个子串的最大值。问最终有几种可能的数字序列。答案对 1e9+7 取模。

Input

第一行两个数 N 和 K。第二行 N 个数，描述一个排列 A。
N,K<=500，

Output

输出一个数，表示答案在模域下的值。

Sample Input

3 2
3 1 2

Sample Output

4

思路

这是一道求区间覆盖方案数的题目
首先第一点，要了解相对位置对答案的贡献
比如313和331和133是3个不同的状态
所谓相对位置就是样例中的312，2相对于1在它的右边，3相对于1和2在它们的左边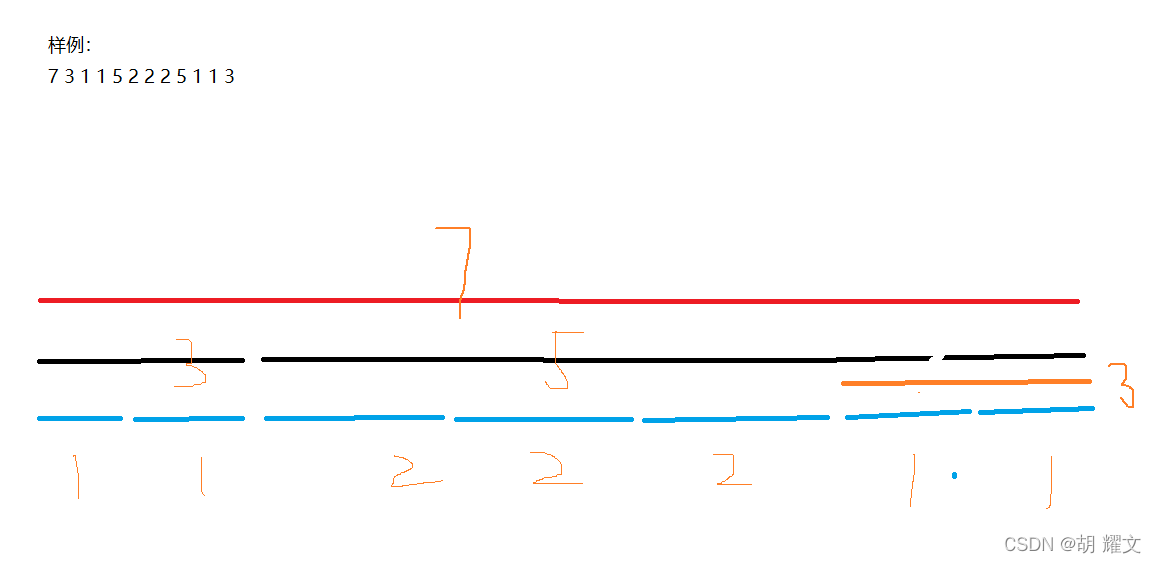

我们把每个数字看成一个区间,问题转化为有n个区间覆盖m次求不同结果状态的数量
我们可以发现，每个数字的方案数=能覆盖的区间方案数之和
即
$$
f(i)=\sum_{k=l}^{k=r}f(k)
$$
比如上述就是$f(3)=f(1)+f(1),f(7)=f(3)+f(5)$

现在我们要考虑如何操作使得答案的统计不重不漏

设$f[i][j]表示选择j个区间并且区间要刚好覆盖到第i个数字的方案数$

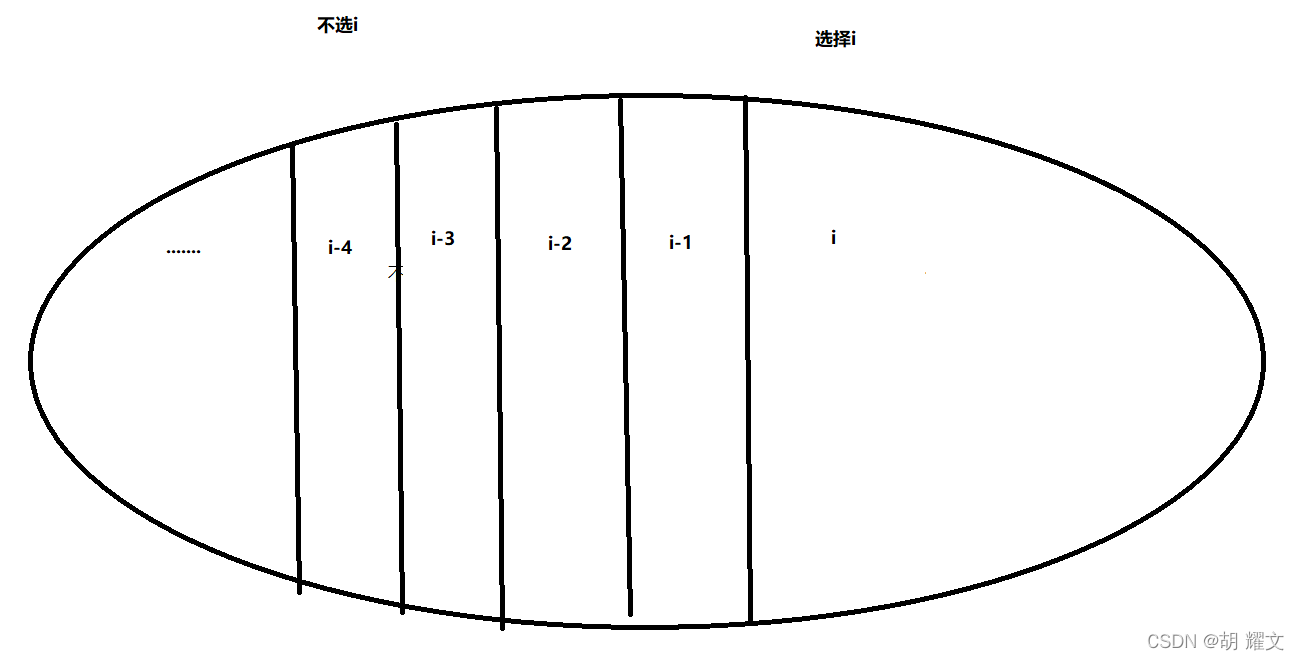
把第j次操作的时候，选择的区间要从i-1，i-2，i-3……覆盖到 i
于是就有了状态转移方程$f[i][j]=\sum_{k=0}^{k=i-1}f[k][j-1]$
但是在最优情况下是不会选单个序列的，也就是说
$f[i-1][j-1]对f[i][j]没有意义，我是不会选择这个操作的，也就是说要保持这个状态我只需要j-1次操作$

前缀和优化
代码如下：

#include<iostream>
using namespace std;
#define int long long
const int N=550;
int f[N][N],a[N],n,m;
const int mod=1e9+7;
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i];
    f[0][0]=1;
    for(int i=1;i<=n;i++){
        int l=i,r=i;
        while(l>1&&a[i]>a[l-1])l--;
        while(r<n&&a[i]>a[r+1])r++;
        for(int j=m;j>=0;j--){
            f[i][j]=(f[i][j]+f[i-1][j])%mod;//我选了j个区间覆盖到i-1了
            if(j==0)continue;
            int sum=0;
            for(int k=l;k<=r;k++){
                sum=(sum+f[k-1][j-1])%mod;
                f[k][j]=(f[k][j]+sum)%mod;
            }
            f[i][j]=(f[i][j]-f[i-1][j-1]+mod)%mod;//减去不符合题意的答案
        }
    }
    int ans=0;
    for(int j=m;j>=0;j--)ans=(ans+f[n][j])%mod;
    cout<<ans;
}

想法：
它为什么是收敛的？也就是说随着可选区间数的不断增加它的方案数最终会趋向0？
小结：
dp牢记

• 问题的转化
• dp状态的定义要清晰！
• dp状态的计算要怎样才能不重复不漏掉